-
10. May 2007 | Trackback | Internet ausdrucken
Die verbotene Zahl
10
Von Wetter habe ich via Netzpolitik folgenden Artikel bekommen. Mein Beitrag zur verbotenen Zahl ist diese OGG-Datei. Es ist der Sound, den ihr hören könnt, wenn ihr die Zahl mal anruft. Hier ist der DTMF-Generator, mit dem ich den Sound erstellt hab.
Leute, die folgende Zahl weitergeben, werden verfolgt:
13256278887989457651018865901401704640
Diese Zahl ist als Schlüssel notwendig, um DVDs der nächsten Generation abspielen zu können. Diese Zahl soll geheim bleiben, damit nur vom DVD-Konsortium lizensierte Software die neuen Bluray- und HD-DVDs abspielen kann. Diese “legale” DVD-Software darf keinerlei Kopiermöglichkeiten bieten.
Warum Kopierschutz-Techniken doch gleich besonders kritisch zu hinterfragen sind, liest Du am besten hier nach.
Der Verwalter des Kopierschutzes, der AACS LA (Advanced Access Content System Licensing Administrator), ist nun bemüht diese Zahl aus dem Netz zu bekommen. Auf Basis des “Digital Millenium Copyright Acts” (DMCA) soll niemand diese Zahl im Zusammenhang mit dem Kopierschutz von Bluray- und HD-DVDs nennen dürfen. Zwischenzeit hat die AACS LA bereits den Schlüssel ausgetauscht, so dass sich künftig erscheinende DVDs mit dieser Zahl nicht abspielen lassen. Aber die neue kommt sicher auch bald raus …
Die Community-Linksammlung digg.com hat Beiträge, die die Zahl beinhalteten, erst gelöscht. Nach vielem Protest sieht der Gründer von digg, Kevin Rose nun davon ab und veröffentlicht die Zahl selbst.
Man dürfte sich darüber freuen, wenn das andere auch tun. Schließlich lässt sich die Zahl auf sehr viele verschiede Arten ausdrücken. Da ist auch sicher eine für Dein Blog dabei!
Etwa zur Basis 16:
09-f9-11-02-9d-74-e3-5b-d8-41-56-c5-63-56-88-c0
Oder binär:
100111111001000100010000001010011101011101
001110001101011011110110000100000101010110
1100010101100011010101101000100011000000Oder als kleine Rechenaufgabe:
41425871524967055159433955941880327 * 320 = HD-DVD
Oder auf Japanisch.
Sehr schön auch die Umrechnung der Hexadezimalzahl in einzelne RGB-Farbwerte, dargestellt als Farb-Fahne (Dank an John von Badmouth):

Die Werte (das +C0 steht für “Crime Zero”):
#09F911 #029D74 #E35BD8 #4156C5 #635688Oder als Morsecode (MIDI-Datei):
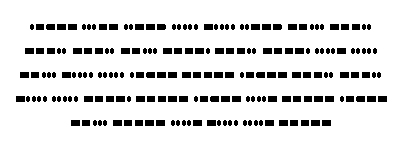
Oder als Braille-Schrift:

Oder als Barcode:

pedro.custodio stellte dieses Zahlenbild unter die CC BY Lizenz:

Dank an Andre Heise aus Lübeck für die Verschlüsselung mit der Enigma-Maschine, die die Deutschen im 2. Weltkrieg nutzten.

Weitere Darstellungen veröffentlicht doch einfach selbst!
Einsortiert: kultur, remix
auch noch zum Thema
10 Responses to “Die verbotene Zahl”
-
Andreas
huh, so wird Codierungstheorie zum Web-event.
-
Hi Julia,
wie kommst du in Hex-Darstellung auf 09-f9-11-02-9d-74-e3-5b-d8-41-56-c5-63-56-88-c0? Mein Taschenrechner liefert 98 47 AF AB 6A 4C FF 59.
Grüße,
Lukas -
haha, ich bin nicht schuld,
ich hab wetter gefragt, ob ich den artikel haben kann, und da sagte er “ja”. dann haben wir es aus der netzpolitik.org-Wordpress-Software raus und in meine WordPress-Software rein kopiert. das hab ich eigentlich auch so gekennzeichnet.
aber ich werde das alles mal auf fehler zu prüfen. schon bei der binären darstellung hab ich mihc gewundert, dass die zahl so kurz ist – bei dieser, die du nennst, könnte man sich wundern, dass die zahl zu lang ist. schon richtig. immerhin sind die zahlen schon durch die netzpolitik.org-BesucherInnen-Meute gegangen, die hätten doch in den Kommentaren was gesagt … oder sind das alles völlig mathematikentleerte laberbacken, die bei netzpolitik.org kommentieren?
könnte ja sein.
-
Hexadezimal: 9F911029D74E35BD84156C5635688C0
Das war also schon richtig. So hab ich das gemacht.
-
Andreas
also Leute, das ist doch voellig egal, ich hatte mit neun so einen Taschenrechner, auf dem ich immer fasziniert zwischen oktal- dezimal und hexadezimalsystem umherrechnete, hier geht es um eine politische Aktion, unabhaengig davon waere es interessant zu wissen, welcher Kodierungsalgorithmus zugrundeliegt und was jene Zahl darin repraesentiert, etwa koennte man auf jenen RSA-Algorithmus tippen, hier waehlt man eine Zahl n=pq, wo p,q grosse Primzahlen sind und einen kleinen Exponenten E und codiert eine Zahl P als C=P^E (mod n), n und E sind publik zu Kodierung. Der eigentliche Dekodierungsschluessel is eine Zahl D, die nur der Dekodierer kennt, so dass DE=k*(p-1)*(q-1)+1 für irgendeine ganze Zahl k, weil dann offenbar C^D=P mod n gilt, der Witz ist, dass sich D in ‘polynomialer’ Zeit aus p und q berechnen laesst, p und q sind aber natuerlich nicht publik. Hat jemand nun also dieses D oder entweder p oder q publik gemacht, ich tippe ja auf D, da das der direkte Schluessel ist, ist die Kodierung natuerlich fuer jeden dekodierbar, oder wurde ein ganz andere Code verwendet, hm.
-
Andreas
Moment, hier noch mal RSA.
-
[…] via Julia / Markus […]
-
[…] Sehr kreativ auch die aktustische Darstellung als DTMF-Tonfolge, mit der sich Telefone steuern lassen von Julia. […]
-
jc
@ Andreas
1. Es handelt sich hier um Kryptographie, nicht um Codierungstheorie.
2. Natürlich ist die es nicht egal, wie die Zahl nun lautet. Schließlich ist das ein Schlüssel.
3. Die zugrundeliegende Verschlüsselung ist AES. Alleine aus der Schlüssellänge von 128 Bit ist es offentsichtlich, dass es sich auf keinen Fall um RSA handeln kann. Heutzutage gilt RSA erst ab einer Verwendung von 1024 Bit langen Schlüsseln als sicher.
4. Für Details siehe das Forum bei Doom9.
-
[…] Sehr kreativ auch die aktustische Darstellung als DTMF-Tonfolge, mit der sich Telefone steuern lassen von Julia. […]



